simple slopes analysis
simple_slopes.RmdSimple Slopes Analysis
Simple slope effects can be plotted using the included
plot_interaction() function. This function takes a fitted
model object and the names of the two variables that are interacting.
The function will plot the interaction effect of the two variables,
where:
- The x-variable is plotted on the x-axis.
- The y-variable is plotted on the y-axis.
- The z-variable determines at which points the effect of x on y is plotted.
The function will also plot the 95% confidence interval for the
interaction effect. Note that the vals_z argument (as well
as the values of x) are scaled by the mean and standard
deviation of the variables. Unless the rescale argument is
set to FALSE.
Here is a simple example using the double-centering approach:
m1 <- "
# Outer Model
X =~ x1
X =~ x2 + x3
Z =~ z1 + z2 + z3
Y =~ y1 + y2 + y3
# Inner Model
Y ~ X + Z + X:Z
"
est1 <- modsem(m1, data = oneInt)
plot_interaction(x = "X", z = "Z", y = "Y", vals_z = c(-1, 1), model = est1)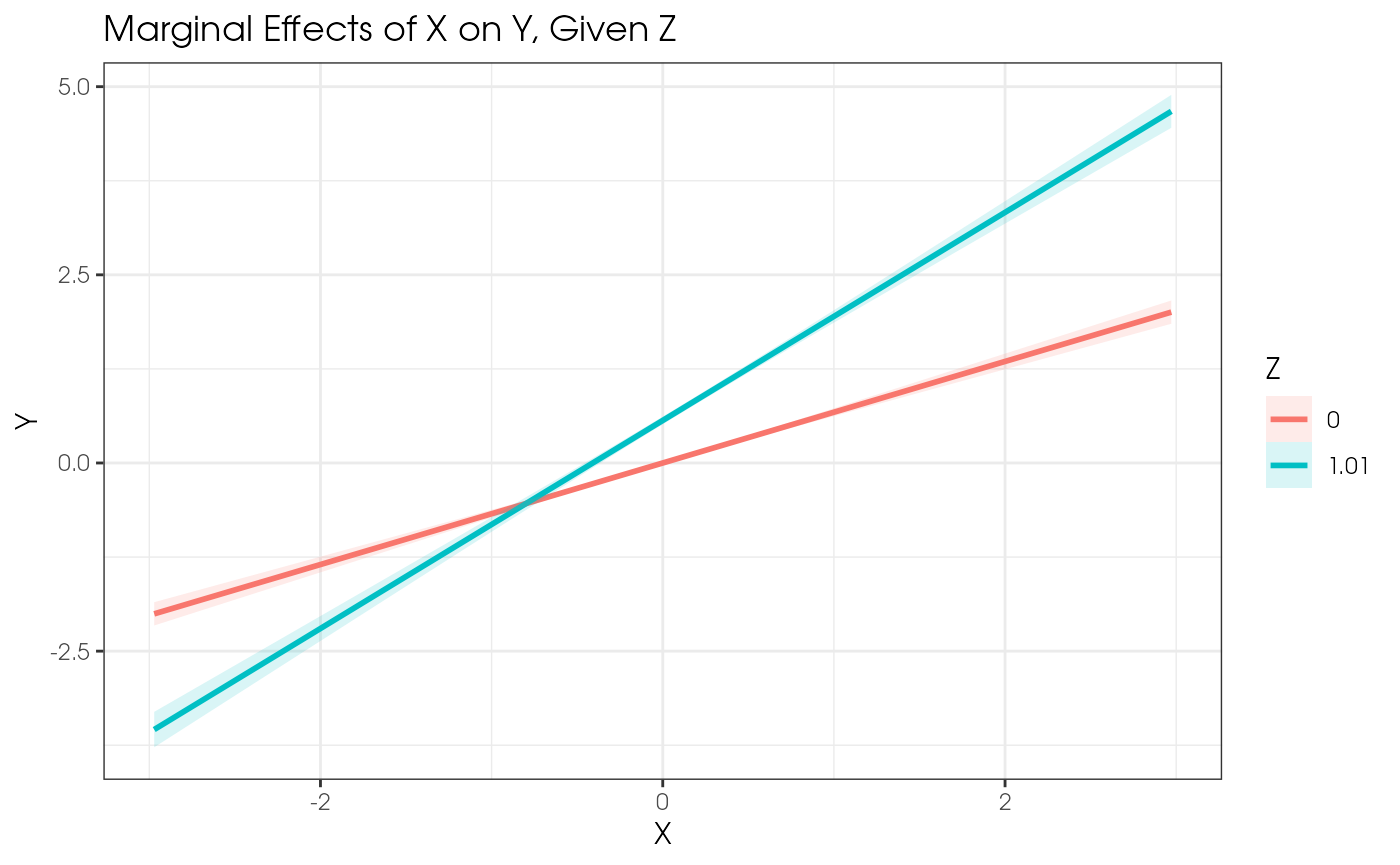
If you want to see the numerical values of the simple slopes, you can
use the simple_slopes() function:
m1 <- "
# Outer Model
X =~ x1
X =~ x2 + x3
Z =~ z1 + z2 + z3
Y =~ y1 + y2 + y3
# Inner Model
Y ~ X + Z + X:Z
"
est1 <- modsem(m1, data = oneInt)
simple_slopes(x = "X", z = "Z", y = "Y", vals_z = c(-1, 1), model = est1)
#>
#> Difference test of Y~X|Z at Z = -1.008 and 1.008:
#> ┌───────────┬───────────┬─────────┬─────────┬───────────────┐
#> │Difference │ Std.Error │ z.value │ p.value │ Conf.Interval │
#> ╞═══════════╪═══════════╪═════════╪═════════╪═══════════════╡
#> │ 1.42 │ 0.054 │ 26.36 │ 0.000 │ [1.31, 1.52] │
#> └───────────┴───────────┴─────────┴─────────┴───────────────┘
#>
#> Effect of Y~X|Z given values of Z:
#> ┌────────┬────────┬───────────┬─────────┬─────────┬────────────────┐
#> │ Y~X │ Z │ Std.Error │ z.value │ p.value │ Conf.Interval │
#> ╞════════╪════════╪═══════════╪═════════╪═════════╪════════════════╡
#> │ -0.033 │ -1.01 │ 0.038 │ -0.88 │ 0.377 │ [-0.11, 0.04] │
#> │ 1.382 │ 1.01 │ 0.038 │ 36.34 │ 0.000 │ [ 1.31, 1.46] │
#> └────────┴────────┴───────────┴─────────┴─────────┴────────────────┘
#>
#>
#> Predicted Y, given Z = -1.01:
#> ┌───────┬─────────────┬───────────┬─────────┬─────────┬─────────────────┐
#> │ X │ Predicted Y │ Std.Error │ z.value │ p.value │ Conf.Interval │
#> ╞═══════╪═════════════╪═══════════╪═════════╪═════════╪═════════════════╡
#> │ -2.97 │ -0.47 │ 0.112 │ -4.17 │ 0.000 │ [-0.69, -0.25] │
#> │ -1.98 │ -0.50 │ 0.076 │ -6.55 │ 0.000 │ [-0.65, -0.35] │
#> │ -0.99 │ -0.53 │ 0.043 │ -12.33 │ 0.000 │ [-0.62, -0.45] │
#> │ 0.00 │ -0.57 │ 0.026 │ -21.61 │ 0.000 │ [-0.62, -0.51] │
#> │ 0.99 │ -0.60 │ 0.048 │ -12.56 │ 0.000 │ [-0.69, -0.50] │
#> │ 1.98 │ -0.63 │ 0.081 │ -7.76 │ 0.000 │ [-0.79, -0.47] │
#> │ 2.97 │ -0.66 │ 0.117 │ -5.67 │ 0.000 │ [-0.89, -0.43] │
#> └───────┴─────────────┴───────────┴─────────┴─────────┴─────────────────┘
#>
#>
#> Predicted Y, given Z = 1.01:
#> ┌───────┬─────────────┬───────────┬─────────┬─────────┬─────────────────┐
#> │ X │ Predicted Y │ Std.Error │ z.value │ p.value │ Conf.Interval │
#> ╞═══════╪═════════════╪═══════════╪═════════╪═════════╪═════════════════╡
#> │ -2.97 │ -3.54 │ 0.120 │ -29.48 │ 0.000 │ [-3.78, -3.31] │
#> │ -1.98 │ -2.17 │ 0.084 │ -25.94 │ 0.000 │ [-2.34, -2.01] │
#> │ -0.99 │ -0.80 │ 0.049 │ -16.30 │ 0.000 │ [-0.90, -0.71] │
#> │ 0.00 │ 0.57 │ 0.026 │ 21.61 │ 0.000 │ [ 0.51, 0.62] │
#> │ 0.99 │ 1.93 │ 0.042 │ 45.91 │ 0.000 │ [ 1.85, 2.02] │
#> │ 1.98 │ 3.30 │ 0.076 │ 43.74 │ 0.000 │ [ 3.16, 3.45] │
#> │ 2.97 │ 4.67 │ 0.112 │ 41.84 │ 0.000 │ [ 4.45, 4.89] │
#> └───────┴─────────────┴───────────┴─────────┴─────────┴─────────────────┘The simple_slopes() function returns a
simple_slopes object. It only has two methods/generics:
print.simple_slopes(), which prints the simple slopes in a
easy-to-read format and as.data.frame.simple_slopes(). The
print() method will not only print the predicted values,
but also significance tests for the difference between the slope at the
lowest value of z and the slope at the highest value of
z, as well as significance tests for the slope of
x at the different values of vals_z.
In the example above, we can see that there is a significant
difference between the slope at at -1 * sd(Z) and
+1 * sd(Z). Note that by default vals_z is
rescaled by the mean and standard deviation of the variable, unless
rescale = FALSE is set. This means that the values of
vals_z are interpreted as standard deviations from the mean
of Z.
If you want to extract the simple slopes as a
data.frame, you can use the as.data.frame()
function:
m1 <- "
# Outer Model
X =~ x1
X =~ x2 + x3
Z =~ z1 + z2 + z3
Y =~ y1 + y2 + y3
# Inner Model
Y ~ X + Z + X:Z
"
est1 <- modsem(m1, data = oneInt)
slopes <- simple_slopes(x = "X", z = "Z", y = "Y",
vals_z = c(0, 1), model = est1)
as.data.frame(slopes)
#> vals_x vals_z predicted std.error z.value p.value ci.upper
#> 1 -2.9713704 0.000000 -2.0043501 0.07897710 -25.37887 4.315370e-142 -1.8495578
#> 2 -1.9809136 0.000000 -1.3362334 0.05265140 -25.37887 4.315370e-142 -1.2330385
#> 3 -0.9904568 0.000000 -0.6681167 0.02632570 -25.37887 4.315370e-142 -0.6165193
#> 4 0.0000000 0.000000 0.0000000 0.00000000 NaN NaN 0.0000000
#> 5 0.9904568 0.000000 0.6681167 0.02632570 25.37887 4.315370e-142 0.7197141
#> 6 1.9809136 0.000000 1.3362334 0.05265140 25.37887 4.315370e-142 1.4394282
#> 7 2.9713704 0.000000 2.0043501 0.07897710 25.37887 4.315370e-142 2.1591423
#> 8 -2.9713704 1.008084 -3.5419750 0.12016032 -29.47708 5.664083e-191 -3.3064651
#> 9 -1.9809136 1.008084 -2.1729185 0.08376085 -25.94194 2.242150e-148 -2.0087503
#> 10 -0.9904568 1.008084 -0.8038620 0.04930659 -16.30334 9.344238e-60 -0.7072229
#> 11 0.0000000 1.008084 0.5651944 0.02615878 21.60630 1.567068e-103 0.6164647
#> 12 0.9904568 1.008084 1.9342509 0.04213438 45.90671 0.000000e+00 2.0168328
#> 13 1.9809136 1.008084 3.3033074 0.07552624 43.73721 0.000000e+00 3.4513362
#> 14 2.9713704 1.008084 4.6723639 0.11167365 41.83945 0.000000e+00 4.8912403
#> ci.lower
#> 1 -2.1591423
#> 2 -1.4394282
#> 3 -0.7197141
#> 4 0.0000000
#> 5 0.6165193
#> 6 1.2330385
#> 7 1.8495578
#> 8 -3.7774849
#> 9 -2.3370868
#> 10 -0.9005012
#> 11 0.5139242
#> 12 1.8516691
#> 13 3.1552787
#> 14 4.4534876